二重积分的求解方法

目录（默认关闭，点击展开）：

展开目录找的更快

点击展开目录

• 二重积分的计算方法
  • 利用直角坐标计算二重积分：
  • 利用极坐标计算二重积分：
• 拓展-概率论部分

二重积分的计算方法

将二重积分化为累次积分

利用直角坐标计算二重积分：

1、若积分区域为：

投影到x轴，再穿线

\[ D=\{(x,y)|a\leq x \leq b ,y_1(x)\leq y \leq y_2(x) \} \] 则有： \[ \iint_{D}{f(x,y)}{dσ}=\int^{a}_{b}{dx}\int^{y_2(x)}_{y_1(x)}{f(x,y)}{dy} \] 2、若积分区域为：

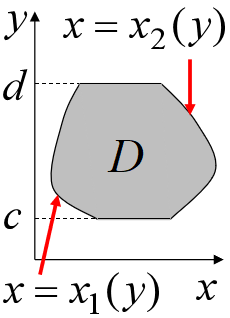\[ D=\{(x,y)|c\leq y \leq d ,x_1(y)\leq x \leq x_2(y) \} \] 则有： \[ \iint_{D}{f(x,y)}{dσ}=\int^{d}_{c}{dy}\int^{x_2(y)}_{x_1(y)}{f(x,y)}{dx} \]

利用极坐标计算二重积分：

若积分区域为：

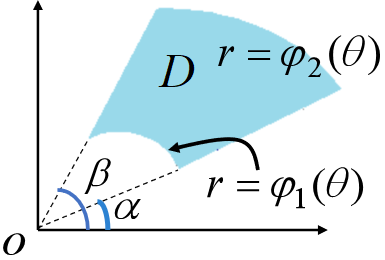\[ D=\{(r,θ)|α\leq θ \leq β ,φ_1(θ) \leq r \leq φ_2(θ) \} \] 则有： \[ \iint_{D}{f(x,y)}{dσ}=\iint_{D}[f(r\cosθ，r\sinθ)r]drdθ \]

\[ =\int^{β}_{α}{dθ}\int^{φ_2(θ)}_{φ_1(θ)}{[f(r\cosθ，r\sinθ)r]}{dr} \]

拓展-概率论部分

概率论部分并没有用到极坐标的计算方法，而且概率论有一个计算打油诗：

计算某个区域的概率时（和联合概率密度有关）

1. 后积先定限
2. 限内画条线
3. 先交写下限
4. 后交写上限

计算边缘概率密度打油诗：

1. 求谁不积谁
2. 不积先定限
3. 限内画条线
4. 先交写下限
5. 后交写上限